La proyección cartográfica es la representación gráfica de la superficie curva de la Tierra sobre una superficie plana (mapa). Los mapas que empleamos para la navegación marítima se llaman cartas náuticas y se conocen también como cartas hidrográficas, marinas y de navegación.
La única manera de representar la superficie terrestre sin deformación o distorsión alguna sería realizando su proyección sobre una superficie esférica, pero mapas o cartas náuticas esféricas no serían en absoluto prácticos. A esta deformación que sufre cualquier representación plana de la superficie terrestre se le llama anamorfosis.
Si la Tierra tuviera forma de cubo, por ejemplo, la representación plana de la misma sería muy simple. Desarrollaríamos las seis caras de un cubo sobre un plano, con dimensiones proporcionales a las caras de la Tierra, según la escala deseada para su representación. En cada cara representaríamos la correspondiente cara del cubo de la Tierra y obtendríamos un mapa exacto y sin deformaciones.
Pero la Tierra es esférica, y para ser más exactos diremos que realmente se trata de un esferoide al ser ligeramente achatada en los polos y abultada en el ecuador. Las proyecciones que se realizan para representar la superficie terrestre sobre un plano se pueden clasificar bajo diferentes criterios, pero los que en náutica más nos pueden interesar son:
- En función de la propiedad que posea la proyección, esta puede ser:
· Equidistante, si conserva las distancias medidas en la Tierra y en la proyección.
· Equivalente, si conserva las superficies.
· Conforme, si conserva las formas y, por lo tanto, los ángulos.
- En función del punto en el que se sitúe el foco u origen de la proyección:
· Gnomónica o centrográfica, si el foco se sitúa en el centro de la Tierra.
· Estereográfica, si el foco se sitúa en el punto de la superficie de la Tierra diametralmente opuesto al punto de tangencia con el plano de proyección.
· Escenográfica, si el foco se sitúa fuera de la Tierra y a una distancia finita de su centro.
· Ortográfica, si el foco se sitúa en el infinito.
- Pero, básicamente, las proyecciones se pueden clasificar en función del tipo de superficie sobre la que se realicen:
· Proyección cilíndrica:
Se usa un cilindro tangente a la esfera terrestre tomando como línea de contacto entre ambos el paralelo del ecuador. El foco de proyección se supone situado en el centro de la Tierra (proyección centrográfica). Al desarrollar el cilindro sobre un plano resultarán los meridianos representados mediante rectas verticales paralelas entre sí y los paralelos como líneas horizontales también paralelas entre sí.
 |
| Fig. 1. Proyección cilíndrica |
La deformación principal es la vertical, ya que suponiendo dos puntos sobre la Tierra a una distancia real vertical entre ellos dada, dicha distancia resulta más grande sobre la representación a medida que los suponemos a mayor latitud sobre la Tierra, manteniendo la misma distancia vertical real. Es decir, la representación se estira enormemente a medida que nos alejamos más del ecuador. Obviamente, resulta imposible representar los polos. Ver figura 2.
En cuanto a la deformación horizontal, sobre la carta cilíndrica la distancia horizontal entre el meridiano de Greenwich y el meridiano del lugar es 60 L millas, independientemente de la latitud l del punto considerado, pues sobre esta carta los meridianos vienen representados por rectas verticales paralelas entre sí. Sin embargo, sobre la superficie de la Tierra, dos meridianos separados por una longitud L están a una distancia real (sobre la Tierra) de 60 L millas solo a la altura del ecuador, o sea, para latitud l = 0°. A medida que aumenta la latitud la distancia horizontal real entre los meridianos disminuye, siendo cero en los polos, donde todos los meridianos confluyen. La distancia real sobre la superficie de la Tierra entre dos lugares sobre dos meridianos distintos separados entre sí una diferencia de longitud ΔL, medida sobre el paralelo de los dos lugares o sobre el paralelo de la latitud media entre ambos, es lo que se llama en navegación apartamiento. Se mide en millas o en minutos de latitud. En la figura 3 se representa claramente este concepto: la diferencia de longitud entre los puntos E y F es la misma que entre A y D y la misma que entre C y B. En todos los casos esa diferencia de longitud es ΔL. Pero la distancia real entre esos puntos, o sea, la longitud en millas de los arcos de circunferencia que los unen (el apartamiento), disminuye a medida que aumenta la latitud. Solo para l = 0° el arco correspondiente, EF, es un arco de círculo máximo (el ecuador) y, por lo tanto, el apartamiento es A = 60 ΔL millas. Pero, en general, a una latitud como la lB, el arco correspondiente, CB, es un arco de círculo menor cuyo radio es r = RT cos(lB), como es evidente a partir del triángulo rectángulo OBO'.
 |
| Fig. 2. Deformación vertical |
En cuanto a la deformación horizontal, sobre la carta cilíndrica la distancia horizontal entre el meridiano de Greenwich y el meridiano del lugar es 60 L millas, independientemente de la latitud l del punto considerado, pues sobre esta carta los meridianos vienen representados por rectas verticales paralelas entre sí. Sin embargo, sobre la superficie de la Tierra, dos meridianos separados por una longitud L están a una distancia real (sobre la Tierra) de 60 L millas solo a la altura del ecuador, o sea, para latitud l = 0°. A medida que aumenta la latitud la distancia horizontal real entre los meridianos disminuye, siendo cero en los polos, donde todos los meridianos confluyen. La distancia real sobre la superficie de la Tierra entre dos lugares sobre dos meridianos distintos separados entre sí una diferencia de longitud ΔL, medida sobre el paralelo de los dos lugares o sobre el paralelo de la latitud media entre ambos, es lo que se llama en navegación apartamiento. Se mide en millas o en minutos de latitud. En la figura 3 se representa claramente este concepto: la diferencia de longitud entre los puntos E y F es la misma que entre A y D y la misma que entre C y B. En todos los casos esa diferencia de longitud es ΔL. Pero la distancia real entre esos puntos, o sea, la longitud en millas de los arcos de circunferencia que los unen (el apartamiento), disminuye a medida que aumenta la latitud. Solo para l = 0° el arco correspondiente, EF, es un arco de círculo máximo (el ecuador) y, por lo tanto, el apartamiento es A = 60 ΔL millas. Pero, en general, a una latitud como la lB, el arco correspondiente, CB, es un arco de círculo menor cuyo radio es r = RT cos(lB), como es evidente a partir del triángulo rectángulo OBO'.
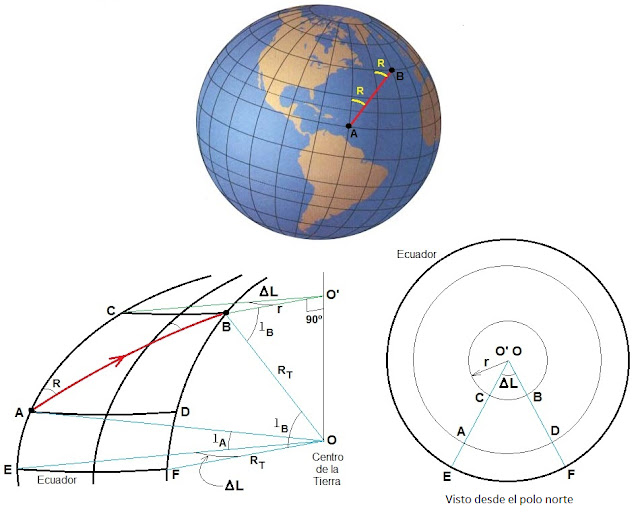 |
| Fig. 3. Concepto de apartamiento |
con ΔL medido en radianes. Pero, puesto que RT es el radio de la Tierra, RTΔL es el arco EF de ecuador entre los dos meridianos en cuestión y su longitud en millas es igual entonces a ΔL expresado en minutos de arco. Por lo tanto, y en resumen, para una diferencia de longitud ΔL dada, el apartamiento correspondiente a una latitud l es:
Despejaremos ΔL de la anterior ecuación para saber la diferencia de longitud que hemos contraído, ΔL = A ÷ cos(l). Pero no hemos navegado a lo largo del paralelo l, sino que nos hemos desplazado cortando paralelos desde el lA al lB, con lo que consideraremos en la ecuación una latitud promedio entre el punto de salida A y el de llegada B, es decir, la latitud media lm, quedando definitivamente la ecuación así:
con la diferencia de longitud ΔL medida en minutos de arco y el apartamiento A en millas.
Acabamos de analizar y comprobar que una carta cilíndrica también tiene deformación horizontal, puesto que a una distancia real sobre la Tierra igual al apartamiento A, en la carta le corresponde una distancia de 60 ΔL y, como hemos visto, ambas cosas solo coinciden sobre el ecuador. La deformación horizontal es entonces nula en el ecuador y aumenta a medida que nos desplazamos hacia los polos. Puesto que la distancia real A es menor que 60 ΔL, deducimos que la carta cilíndrica produce un estiramiento en la dirección horizontal que aumenta a medida que nos alejamos del ecuador.
Acabamos de analizar y comprobar que una carta cilíndrica también tiene deformación horizontal, puesto que a una distancia real sobre la Tierra igual al apartamiento A, en la carta le corresponde una distancia de 60 ΔL y, como hemos visto, ambas cosas solo coinciden sobre el ecuador. La deformación horizontal es entonces nula en el ecuador y aumenta a medida que nos desplazamos hacia los polos. Puesto que la distancia real A es menor que 60 ΔL, deducimos que la carta cilíndrica produce un estiramiento en la dirección horizontal que aumenta a medida que nos alejamos del ecuador.
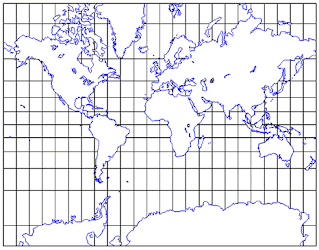 |
| Fig. 4. Mapa resultante de la proyección cilíndrica centrográfica |
La proyección cilíndrica centrográfica así concebida no sería válida para la navegación, ya que aunque evidentemente una derrota loxodrómica quedaría representada por una recta, dado que los meridianos se proyectan paralelos entre ellos, sin embargo no sería conforme al no corresponderse los ángulos (rumbos) en la representación con los reales sobre la Tierra por el excesivo estiramiento vertical. Pero, demostremos esta no conformidad utilizando de nuevo la figura 3:
Supongamos que queremos navegar del punto A al punto B, con lo que deberíamos poner rumbo R. Consideremos que la distancia entre A y B es pequeña con relación al tamaño de la Tierra, situación que sucede en la mayoría de nuestras navegaciones. Entonces el triángulo curvo sobre la superficie de la Tierra (que no es un triángulo esférico porque algunos de sus lados no son arcos de círculo máximo) lo podemos considerar plano. Se trata entonces de un triángulo rectángulo que tiene como hipotenusa la distancia navegada desde A hasta B y como catetos el apartamiento A = CB y el arco de meridiano cuya longitud (en millas) es Δl (en minutos de arco), siendo Δl la diferencia de latitud entre el punto de llegada B y el de salida A. Por lo tanto, según la trigonometría plana, resulta que:
con ΔL y Δl en minutos de arco. Y, sin embargo, si calculamos el rumbo sobre la carta cilíndrica obtendremos el siguiente resultado, que es diferente al anterior:
con ΔL en minutos de arco y RT en millas. En consecuencia, la proyección cilíndrica no es conforme y como consecuencia es inútil para la navegación, dado que los ángulos R sobre la superficie terrestre y sobre la carta vemos que son desiguales.
El concepto de apartamiento y la ecuación que hemos visto antes, A = ΔLcos(l), son útiles en los cálculos de navegación por estima cuando la distancia navegada no sea muy grande (inferior a unas 300 millas náuticas), al poder considerar el triángulo de estima ABC como un triángulo plano sin cometer error significativo en los cálculos de estima.
El concepto de apartamiento y la ecuación que hemos visto antes, A = ΔLcos(l), son útiles en los cálculos de navegación por estima cuando la distancia navegada no sea muy grande (inferior a unas 300 millas náuticas), al poder considerar el triángulo de estima ABC como un triángulo plano sin cometer error significativo en los cálculos de estima.
La proyección cilíndrica más importante es la proyección de Mercator o mercatoriana, denominada así al haber sido ideada por Gerardus Mercator en 1569 y es la más utilizada desde el siglo XVIII para la navegación, porque realizando unos cambios de concepción a la proyección cilíndrica centrográfica, además de representarse una derrota loxodrómica como una recta, cosa que sí se podía, consiguió que también fuera conforme, pudiéndose trazar rumbos que se correspondieran con los reales sobre la Tierra. Más adelante veremos cómo lo hizo.
· Proyección cónica:
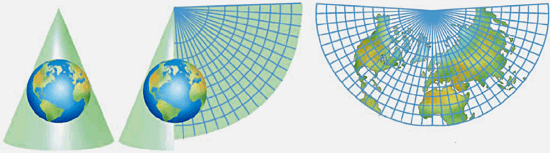 |
| Fig. 5. Proyección cónica |
La distorsión aumenta más cuanto más se aleje del paralelo estándar. Las proyecciones cónicas se utilizan para zonas de latitudes medias.
Este tipo de proyección, sin realizar sobre él ningún tipo de modificación, no resulta útil para la navegación, ya que al no mantener las direcciones correctamente, no se puede trazar los rumbos.
 |
| Fig. 7. Tipos de proyecciones acimutales |
De aplicación náutica resulta el tipo más común de proyección acimutal denominada gnomónica o centrográfica, cuya proyección se realiza desde el centro del globo terráqueo. Con este concepto los círculos máximos se proyectan como líneas rectas en el plano de proyección (recordemos que el camino más corto entre dos puntos de la Tierra es el arco de círculo máximo que los une). Los círculos menores forman secciones cónicas en el plano de proyección. Esto es debido a que los círculos menores forman con el centro de la esfera un cono mediante las generatrices y la intersección del cono forma las cónicas correspondientes.
La proyección gnomónica, en función del punto de tangencia del plano de proyección con la esfera terrestre, puede ser:
- Polar o directa, si el punto de tangencia es un polo. Veríamos entonces que los meridianos quedarían representados por rectas radiales con centro en el polo y distanciadas ángulos iguales. Los paralelos se representarían mediante circunferencias concéntricas, aumentando su separación a medida que se distancian del polo.
- Ecuatorial, meridiana o transversa, si el plano fuera tangente a un punto del ecuador. Los meridianos serían paralelos distanciados cada vez más entre ellos a medida que se separan del punto de tangencia. Los paralelos serían curvas hiperbólicas cóncavas hacia el polo más cercano (polo elevado), que aumentarían su separación a medida que se alejasen del punto de tangencia, y el ecuador una línea perpendicular a los meridianos.
- Oblicua u horizontal, si la tangencia se situara en cualquier otro punto. Los meridianos serían rectas convergentes hacia el punto de proyección del polo, los paralelos estarían representados por parábolas, hipérbolas o elipses, según la latitud, y el ecuador por una recta perpendicular al meridiano central.
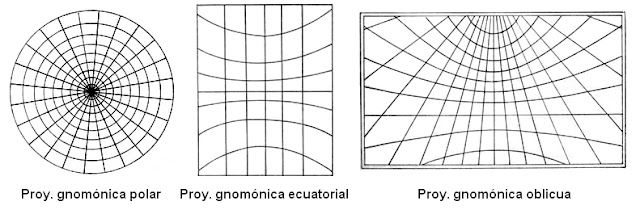 |
| Fig. 8. Proyecciones acimutales gnomónicas |
Al quedar trazados los círculos máximos como líneas rectas en las proyecciones gnomónicas, las derrotas ortodrómicas (de círculo máximo) quedan representadas mediante una recta, por lo que las cartas gnomónicas son útiles en este tipo de navegaciones, y las loxodrómicas (de rumbo constante) se representan mediante una línea curva, por lo que no se utilizan en navegaciones loxodrómicas.
Cartas mercatorianas.
Como dijimos con anterioridad, la proyección cilíndrica centrográfica no nos sirve para navegar al no ser conforme, es decir, al no corresponderse un ángulo real sobre la superficie de la Tierra con su representación en la carta. Mercator encontró la forma de modificarla para convertirla en conforme. Veamos el razonamiento sobre la figura 9.
Si queremos navegar desde el punto A al punto B, el rumbo necesario es R. Si suponemos que la distancia entre A y B es pequeña comparada con el tamaño de la Tierra, el triángulo curvo ABC que se forma sobre la superficie de la Tierra lo podemos considerar plano. Se trata entonces de un triángulo rectángulo que tiene como hipotenusa la distancia navegada desde A hasta B y como catetos el apartamiento A y el arco de meridiano AC, cuya longitud (en millas) es AC = Δl (en minutos de arco), siendo l la diferencia de latitud entre el punto de llegada B y el de salida A. Y la trigonometría plana nos dice que: tg(R) = A ÷ Δl = ΔL cos(l) ÷ Δl.
Puesto que en la proyección cilíndrica la separación horizontal es ΔL, en lugar del apartamiento A, lo que necesitaremos hacer es modificar la proyección de forma que a una distancia vertical real Δl le corresponda una distancia vertical sobre la carta h tal que, al aplicar la trigonometría, nos resulte el mismo ángulo R, es decir, tendremos que modificar el estiramiento vertical de la carta.
Igualando las expresiones obtenidas anteriormente que definen tg(R), sobre la esfera terrestre y sobre la carta, calcularemos el valor que ha de tener h para que la carta sea conforme:
Hasta aquí habríamos convertido la carta cilíndrica centrográfica en conforme a nivel matemático, pero ¿cómo realizó Mercator la modificación de la proyección cilíndrica de forma que en el entorno de un punto de latitud l, a una distancia vertical real Δl, le corresponda una distancia h = Δl ÷ cos(l) en la proyección?
Pues en lugar de utilizar un único cilindro tangente a la Tierra a lo largo del ecuador, como se hacía en la proyección cilíndrica, en la proyección mercatoriana se divide el meridiano en un número infinito de partes infinitesimales, cada una correspondiente a una diferencia de latitud infinitesimal dl (figura 10), a cada una de las cuales se le hace corresponder un cilindro sobre el que se proyecta desde el centro de la Tierra. Después, cuando cada uno de estos cilindros infinitesimales tiene ya proyectados sobre él las diferentes partes de la Tierra, se considera otro cilindro que, al igual que en el caso de la proyección cilíndrica, rodea a la Tierra tangente al ecuador. Se proyectan ahora los cilindros pequeños sobre este último horizontalmente, no produciéndose, por lo tanto, deformación adicional alguna. Finalmente, cortando este cilindro por su generatriz y desarrollándolo se obtendrá una carta mercatoriana que, como vamos a ver seguidamente, verifica la condición necesaria para ser conforme.
La distancia AB vertical (sobre el meridiano) real es ahora d = RT dl (con dl en radianes) o, lo que es lo mismo, d = dl con dl en minutos de arco (que son millas, pues el meridiano es un círculo máximo de la Tierra). Sobre la proyección mercatoriana es h. Ahora bien, puesto que dl es infinitamente pequeña, ABC puede considerarse como un triángulo rectángulo en el que se tiene:
 |
| Fig. 10. Modificación de Mercator sobre la proy. cilíndrica |
que era, precisamente, la condición necesaria para que rumbos medidos sobre la superficie de la Tierra coincidieran con rumbos medidos sobre la carta. Así que la proyección mercatoriana es conforme y para ello hemos modificado la proyección cilíndrica consiguiendo que la separación entre dos paralelos dados aumente, cuando son representados sobre la carta, como 1 ÷ cos(l), o lo que es lo mismo como la sec(l), en lugar de aumentar como tg(l), como sucedía en la proyección cilíndrica. El resultado final es una carta mercatoriana (figura 11) en la que existe la misma deformación horizontal que en la carta cilíndrica, pero en la que la deformación vertical es diferente (menor) y es la necesaria para que la carta sea conforme.
 |
| Fig. 11. Carta mercatoriana |
Latitudes aumentadas.
Se llama latitud aumentada a la
dimensión en millas que tiene un arco de meridiano, desde el ecuador hasta una
latitud dada, medido en el plano de proyección. En otras palabras, latitud
aumentada es la dimensión que adquiere la latitud al ser proyectada sobre un
plano. La latitud aumentada se mide en minutos de arco de círculo máximo, o sea en millas, desde el ecuador hasta el paralelo de la latitud
considerada. Se denomina así porque su valor crece rápidamente con el aumento de la latitud. En efecto, para l = 0° tenemos la = 0 y para l = 90° tenemos que la es infinita.
A un punto sobre la superficie de la Tierra a una latitud l, le corresponde sobre la carta mercatoriana una latitud aumentada la. Para obtener el valor de la en función de l, nos basaremos de nuevo en la figura 10, en la que la será el resultado de sumar las alturas h de todos los cilindros infinitesimales existentes entre el ecuador y el cilindro correspondiente al punto de latitud l en cuestión. Esta suma de elementos infinitesimales se resuelve mediante una integral definida:
A un punto sobre la superficie de la Tierra a una latitud l, le corresponde sobre la carta mercatoriana una latitud aumentada la. Para obtener el valor de la en función de l, nos basaremos de nuevo en la figura 10, en la que la será el resultado de sumar las alturas h de todos los cilindros infinitesimales existentes entre el ecuador y el cilindro correspondiente al punto de latitud l en cuestión. Esta suma de elementos infinitesimales se resuelve mediante una integral definida:
Si utilizamos logaritmos decimales en puesto de
neperianos, deberemos dividir por log e:
Para expresar la en millas, tendremos que indicar el radio de la Tierra RT también en millas:
Dividiendo por log e obtendremos la expresión de la en millas:
Finalmente, para obtener una expresión más exacta deberemos tener en cuenta que la Tierra no es exactamente una esfera, sino que está achatada por los polos, para lo que debemos añadir la corrección -23sin(l), de la que no viene al caso aquí su demostración. Por
lo tanto, la ecuación final que nos da el valor de la latitud aumentada la, en millas, medida sobre una carta mercatoriana desde la representación del ecuador hasta la representación de un punto de latitud l es:
Los valores de la latitud aumentada la en función de la latitud l se encuentran tabulados en muchos libros de Tablas Náuticas. Se puede descargar la Tabla de Latitudes Aumentadas, también denominada Tabla de Partes Meridionales. El uso de esta tabla es muy sencillo. Mejor veámoslo con un ejemplo:
Supongamos que queremos calcular la latitud aumentada la sobre la carta mercatoriana de un punto cuya latitud sobre la Tierra es l = 32° 47' N. Buscamos en la tabla la cifra que aparece en la intersección de la fila correspondiente a los grados de latitud (32°) con la columna de las decenas de minutos (40'), y observamos que nos arroja el valor de 2063,3'. Ahora solo nos quedará sumarle a esa cifra la que aparece en la intersección entre la fila correspondiente a los 32° con la columna correspondiente a las unidades de minuto (7'), que vemos que nos muestra 8,3'. Por lo tanto, la latitud aumentada correspondiente a l = 32° 47' N será la = 2063,3' + 8,3' = 2071,6' (millas) N. Si los minutos de latitud tuvieran algún decimal, simplemente interpolaríamos en la tabla. Evidentemente, la latitud aumentada tiene el mismo signo N o S que la latitud.
En otro artículo de este blog puedes obtener el valor de la latitud aumentada correspondiente a una latitud dada de forma online.
El concepto de latitud aumentada sobre la carta Mercator es fundamental en los cálculos de navegación por estima cuando la distancia navegada es grande (superior a 300 millas náuticas), dado que en estos casos no podemos considerar el triángulo de estima sobre la Tierra como un triángulo plano y utilizar el concepto de apartamiento, puesto que de hacerlo incurriríamos en errores de cálculo inadmisibles.
Conclusiones finales:
- Para navegaciones hasta 300 millas podremos resolver el triángulo de estima directamente sobre la superficie terrestre considerándolo como un triángulo plano y empleando, por lo tanto, la diferencia de latitud Δl entre los puntos de salida y de llegada y el apartamiento A entre ellos, ambos valores expresados en minutos de arco de círculo máximo, o sea, en millas.
- Para navegaciones superiores a 300 millas deberemos resolver el triángulo de estima sobre la carta mercatoriana empleando la diferencia de latitudes aumentadas Δla y la de longitud ΔL entre los puntos de salida y de llegada, ambas expresadas también en millas.
Clasificación de las cartas según la escala.
Escala es la relación entre la magnitud representada y la real. Se expresa en base a la unidad y, por ello, en el numerador aparece siempre la unidad cuando la magnitud representada es menor que la real, como ocurre en cualquier representación de la Tierra.
En el caso de las cartas náuticas, la escala viene dada por la relación entre el radio de la esfera imaginaria con la que se ha representado la carta y el radio de la Tierra, es decir, escala = r:R, en donde a r se le da el valor 1, de tal manera que si por ejemplo nos encontramos con una carta a escala 1:50.000, significa que el radio de la Tierra es 50.000 veces mayor que el radio de la esfera con la que se ha representado la carta.
Tratando de buscar la escala apropiada para representar la extensión de la zona que se trata de cartografiar, las cartas náuticas se dividen en cuatro grupos principales:
a) Cartas generales. Abarcan una gran extensión de costa y mar y están destinadas a la navegación oceánica. Su escala es muy pequeña y oscila entre 1:30.000.000 y 1:3.000.000.
b) Cartas de arrumbamiento. Se utilizan para distancias de tipo medio. Sus escalas están comprendidas entre 1:3.000.000 y 1:200.000.
c) Cartas de navegación costera o cuarterones. Sirven para navegar a la vista de la costa. Tienen escalas comprendidas entre 1:200.000 y 1:50.000. La carta de escala 1:50.000 es la que contiene el máximo detalle posible de la geografía y del fondo marino de la zona que comprenda, por lo que se deberán utilizar cartas de esta escala para navegar en las cercanías de la costa.
d) Aproches (cartas de recalada o aproximación). Los aproches son cartas de escala entre 1:50.000 y 1:25.000 que sirven para facilitar al navegante la aproximación a los puertos, canales angostos o a otros accidentes geográficos que por su importancia requieran más detalle.
e) Portulanos. Son cartas de escala mayor de 1:25.000 que muestran con todo detalle una pequeña extensión de costa y mar, como pueden ser puertos, radas, ensenadas, fondeaderos, etc.
En ocasiones, dentro del marco de una carta de navegación costera se inserta a una mayor escala, 1:25.000 o superior, la representación de un lugar, puerto, fondeadero, bahía, isla, etc., que por su menor importancia no se le ha dedicado un portulano aparte. A este portulano dentro de otra carta se le llama cartucho.
A las cartas que representan grandes extensiones, como las generales y las de arrumbamiento, se las conoce como cartas de punto menor; y a las cartas que representan extensiones menores, como las de navegación costera, aproches y portulanos, se las denomina cartas de punto mayor.
Información proporcionada por las cartas.
La interpretación de la inmensa cantidad de detalles y símbolos que se encuentran en una carta es importantísima, dado que ello entraña la seguridad del barco y de la tripulación.
A continuación, un resumen de los más relevantes y generales:
· Faros. Representados mediante una lagrimita de color negro. La situación exacta del faro está en el punto de donde arranca la lágrima. También se representan las luces de entrada en puerto, que se representan mediante un pequeño círculo de color negro con la inicial V (luz verde) o R (luz roja).
· Sondas. Profundidades del mar a intervalos tan pequeños como lo permita la claridad y la escala. La unidad empleada es el metro para sondas y elevaciones.
· Veriles. Son líneas continuas que unen los puntos de igual profundidad (isobáticas) para llevar la derrota de un buque de acuerdo con su calado.
· Calidad del fondo. Indica la naturaleza del fondo cerca de la costa, en fondeaderos y zonas de no mucha profundidad.
· Peligros submarinos. Todo lo que constituya un peligro para la navegación como rocas sumergidas a poca profundidad o rocas que velan, naufragios, arrecifes, bajos, tuberías y tendidos eléctricos submarinos, etc.
· Línea de costa. Todo el contorno de la costa con su forma, orientación, aspecto y características (alta, escarpada, rocosa, de arena, etc.), cabos, bahías, islas e islotes, ríos con sus desembocaduras, puertos con sus muelles o espigones, ciudades costeras, fondeaderos, etc. Es conveniente señalar aquí que una habilidad importante del navegante es la de reconocer en la carta la costa que tiene a la vista.
· Derrotas y enfilaciones. Derrota recomendada en canales, pasos, entradas a ciertos puertos, con indicación de las enfilaciones a puntos fijos para mantenerse en la derrota, así como los dispositivos de separación de tráfico, etc.
· Señalización y objetos visibles. Ubicación de los faros con leyendas que indican el número de destellos u ocultaciones, su frecuencia y su altura, balizas, luces, boyas, pontones fondeados, piscifactorías, plataformas en alta mar, etc. Así mismo, también objetos fijos terrestres visibles desde el mar, como cerros, puntas quebradas, torres, edificios, etc.
· Mareas y corrientes. Valores del establecimiento del puerto, amplitud de la marea en sicigias y niveles de reducción de sondas y alturas terrestres en bahías, puertos, caletas y fondeaderos. Indicación de la dirección, sentido e intensidad de las corrientes reinantes de la zona, así como de las corrientes generadas por las mareas.
· Nombres geográficos. Todos los accidentes topográficos e hidrográficos están indicados por sus nombres propios, como pueden ser: puertos, cabos, puntas, islas, cerros, etc.
· Declinación magnética y su variación anual. Llamada también variación magnética y se representa por dm o V. Se define como el ángulo que forma el meridiano geográfico y el meridiano magnético. La declinación magnética varía según el lugar en el que nos encontremos y con el paso del tiempo. Las cartas náuticas, por lo tanto, además del valor de la declinación magnética para una zona y en un determinado año, expresan también su incremento o decremento anual.
Existe aproximadamente un millar de símbolos y abreviaturas empleados en las cartas náuticas. Todos se encuentran recogidos en la Publicación INT-1 o Publicación Especial nº 14 del Instituto Hidrográfico de la Marina.
Se puede descargar una publicación del SHOA donde también aparecen estos símbolos y abreviaturas.
Cartas en blanco.
Cuando realizamos largas navegaciones sin tener costa a la vista, como sucede en las navegaciones oceánicas, ya no podemos utilizar las técnicas de navegación costera (demoras, enfilaciones, etc.). Y navegar solo por estima nos conduciría a enormes errores, dado que podrían pasar días antes de volver a observar referencias de tierra para corregir nuestra situación estimada. Por lo tanto, en este tipo de navegaciones es en las que tenemos que utilizar las técnicas de navegación astronómica para efectuar las correcciones de la estima.
Necesitamos la carta de la zona en la que navegamos para representar nuestras posiciones, trazar rectas de altura, etc. Pero necesitamos una carta de punto suficientemente grueso para poder trabajar con precisión, o sea, que abarque solo unas pocas millas
alrededor de nuestra posición y en la que todo sería océano y no aparecería tierra por ningún lado. A este tipo de carta mercatoriana se le llama carta en blanco. Estas cartas, como cualquiera, deberán tener una escala de longitudes y otra de latitudes. Estas últimas deformadas (aumentadas) más o menos en función de lo lejos que nos encontremos del ecuador. Los paralelos estarán separados en función de la secante de la latitud media de la carta, como ya vimos con anterioridad al estudiar la proyección de Mercator.
Estas cartas en blanco se pueden adquirir en tiendas especializadas. Son válidas para cualquier zona de la Tierra y la única diferencia entre una carta en blanco y otra es el rango de latitudes que cubre y según sea este, así será la deformación vertical que tenga. Cuanto mayor sea la latitud, mayor será la separación en centímetros que tengan sobre la carta dos puntos sobre el mismo meridiano y con una diferencia fija de latitud entre ellos, aunque la distancia real en millas que los separa es, obviamente, la misma.
Pero no es necesario recurrir a la compra de estas cartas en blanco y, como alternativas, se puede optar por cualquiera de estas posibilidades:
1ª. Construir nosotros mismos las cartas en blanco.
En una hoja en blanco, preferiblemente cuadriculada o milimetrada, trazamos una línea horizontal que representará la latitud más baja de nuestra carta. Partiendo de ella, hacia arriba, trazaremos verticalmente los meridianos equidistantes en la medida y separación de la ΔL que queramos representar (ver figura 12). A partir del punto de corte del primer meridiano con el primer paralelo, trazaremos un ángulo con este primer paralelo igual a la latitud media de la carta que vamos a construir (en este ejemplo será la latitud de 36° 30' N = 36,5° N). Este lado del ángulo cortará a los meridianos en los puntos a, b, c, d, etc. Con el compás y haciendo centro en el vértice del ángulo, llevaremos las distancias hasta a, b, c, d, etc., hasta el primer meridiano. A partir de los puntos de corte que se producen, trazaremos los diferentes paralelos horizontales y así habremos construido la carta en blanco, también denominada carta de fortuna, apropiada para las proximidades del paralelo de latitud 36° 30' N.
 |
| Fig. 12. Construcción de una carta mercatoriana en blanco |
2ª. Utilizar las plotting sheets americanas.
Estas hojas nos facilitan aún más la construcción de una carta en blanco, dado que incorporan una rosa con el fin de evitar el uso del transportador de ángulos. Además, traen ya dibujada una escala vertical de latitudes que abarca 1° de latitud por encima y por debajo del paralelo central. Para obtener la división correspondiente a 1° de longitud, trazaremos una línea vertical que corte a la rosa donde lo haría la línea oblicua dibujada formando un ángulo l, igual a la latitud, con la horizontal y que, utilizando la rosa, ya no es necesario dibujar.
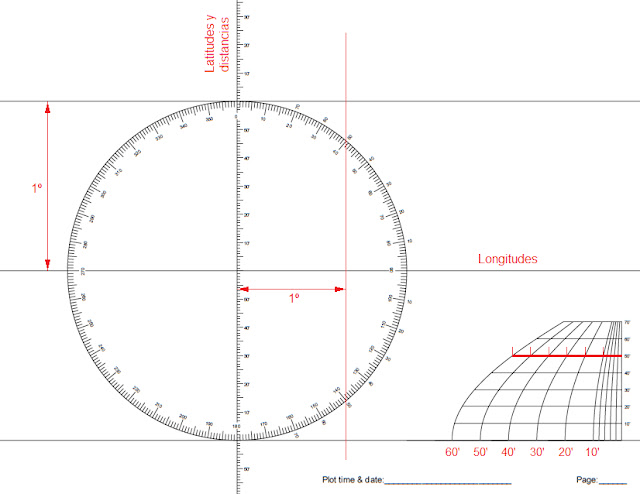 |
| Fig. 13. Plotting sheet americana |
Si lo deseas, puedes descargar e imprimir la plotting sheet.
Publicado por Manuel Pastor.
Comparte este artículo en redes sociales:
Para ir a "Índice de contenidos"...




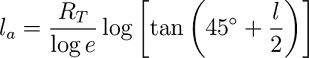

.png)
.png)

10 comentarios:
Genial! muy completo.
A Anónimo
Gracias.
Excelente artículo Sr. Pastor y muchísimas gracias por su generosidad compartiendo estos conocimientos.
@Anónimo
Muchas gracias a usted por su amable comentario. Un saludo.
me gustaria saber esa constante 7915.7 de donde sale, o como se calcula
gracias
@Anónimo
Ese valor resulta de dividir el radio de la Tierra (RT) entre log (e), donde e (también llamado número de Euler) es una constante, cuyo valor es aproximadamente 2,71828. Con lo cual, 3437,746 ÷ log (e) = 3437,746 ÷ 0,4343 = 7915,7. Un saludo.
Buenos días sr M Pastor, le agradezco mucho su respuesta, pero sigo sin entender la respuesta, dice ud, que el Rt se divide entre el logaritmo " e " cuyo valor es 2.71828, entonces si divido 3437.74 entre 2.71828 a mi me sale 1264,66, y ud pone 3437,746 / 0,4343 y digo yo de donde sale ese 0,4343
doy por hecho que tiene que haber un calculo que lo indique, pero hasta ahí mis conocimientos no llegan muchas gracias otra vez y disculpe la molestia
@Anónimo
Molestia ninguna, en absoluto. Te explico:
2,71828 es el valor del número "e" (valor constante), pero NO es el valor de log (e) (logaritmo de "e"). Si calculas el log (e), es decir, el log (2,718289), verás que resulta ser 0,4343.
Por lo tanto, RT ÷ log (e) = 3437,746 ÷ 0,4343 = 7915,7.
Espero habértelo aclarado. Un saludo.
Perfectamente aclarado,, anoche pensando es esto intui que que lo que yo deberia hacer es poner en la calculadora Log de 2.71828 y que posiblemente me saldría ese 0,4343, pero no lo hice preferi esperar a hoy para ver su respuesta, y efectivamente comprendo que es que yo no sabia interpretar esa ecuacion, muchas gracias,
esta consulta la he hecho porque ayudando a amigos y compañeros, a preparar los exámenes de Patronn de Yate y C.Y en algunos ejercicios salen con distancias grandes donde hay que aplicar las latitudes aumentadas, y sabemos el famodo 7915,7 pero lo de siempre si alguien pregunta - muchos lo hacen - de donde sale esa contante, pues sinceramente, nos quedamos en blanco, por lo menos yo, una vez pregunte a Luis Mederos en su foro de Rodamedia, y dijo en la página tal del libro está explicado, solo hay que hacer una simple ecuación, pero no explico esa simple ecuación como era, Ud. ahora si me lo ha explicado muy bien,
muchas gracias y le felicito por esta página es muy interesante, y se la recomiendo a muchos amigos,
buen día
@Anónimo
Celebro que haya quedado aclarada tu duda y muchas gracias por tu comentario acerca de mi blog.
Un saludo.
Publica tu comentario: