Las distancias a faros o a ciertos puntos elevados de la costa se pueden calcular averiguando su ángulo vertical, también denominado ángulo sextantal al ser el sextante el instrumento de medida. Una vez obtenido el ángulo, y conociendo la altura sobre el nivel del mar del punto (mediante la información facilitada por los derroteros, libros de faros, etc.), podremos calcular la distancia a ese punto. Si se tiene además la demora a ese u otro punto de la costa, se logra determinar la situación por demora y distancia.
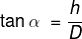
; y dado que la inversa de la tangente es la cotangente, entonces:
; dado que la altura h en las publicaciones náuticas nos vendrá dada en metros, resultará:
; pero como la distancia D nos interesará conocerla en millas náuticas (1 milla náutica = 1852 metros), la ecuación definitiva quedará así:
(1)
Si no se quiere emplear la anterior fórmula de la cotangente, también se podría emplear la siguiente ecuación, pero teniendo en cuenta indicar el ángulo α en minutos de arco y decimales:
(2)
La fórmula (2) es muy exacta para ángulos pequeños, es decir, para distancias apreciables, pero conforme va aumentando el ángulo (disminuyendo la distancia), el error va aumentando ligeramente, aunque resulta perfectamente despreciable. La fórmula (1) es totalmente exacta con cualquier ángulo, dado que emana directamente del propio teorema de Pitágoras.
Veamos un ejemplo:
Determinar la posición en la que se encuentra una embarcación navegando a Ra = 217° (Ct = -12°) al tomar el ángulo vertical del faro de Espartel de 0° 35,1', sabiendo que su altura es de 95 metros y teniendo en ese mismo instante una marcación del faro de 275°.
Rv = Ra + Ct = 217 + (-12) = 205°; Dv = Rv + M = 205 +275 = 480 (-360) = 120°; Opuesto = 300°.
D = h x cotg α = 95 x cotg (0° 35,1') ÷ 1852 = 5,02 millas náuticas.
O también, mediante la segunda fórmula:
D = 1,856 x 95 ÷ 35,1 = 5,02 millas náuticas.
Trazando en la carta náutica la recta correspondiente a la demora verdadera de 300° desde el faro de Espartel, y un arco de circunferencia con centro en dicho faro y radio igual a la distancia calculada de 5,02 millas, la intersección de las dos líneas nos dará la situación:
En la sección "Cálculos online" de este blog encontrarás el artículo "Distancia a un punto mediante ángulo vertical" en el que podrás realizar cálculos.
Por trigonometría plana sabemos que, en un triángulo rectángulo, la tangente de un ángulo es la relación que existe entre el cateto opuesto y el cateto contiguo.
Por lo tanto:
; y dado que la inversa de la tangente es la cotangente, entonces:
; dado que la altura h en las publicaciones náuticas nos vendrá dada en metros, resultará:
(1)
(2)La fórmula (2) es muy exacta para ángulos pequeños, es decir, para distancias apreciables, pero conforme va aumentando el ángulo (disminuyendo la distancia), el error va aumentando ligeramente, aunque resulta perfectamente despreciable. La fórmula (1) es totalmente exacta con cualquier ángulo, dado que emana directamente del propio teorema de Pitágoras.
Veamos un ejemplo:
Determinar la posición en la que se encuentra una embarcación navegando a Ra = 217° (Ct = -12°) al tomar el ángulo vertical del faro de Espartel de 0° 35,1', sabiendo que su altura es de 95 metros y teniendo en ese mismo instante una marcación del faro de 275°.
Rv = Ra + Ct = 217 + (-12) = 205°; Dv = Rv + M = 205 +275 = 480 (-360) = 120°; Opuesto = 300°.
D = h x cotg α = 95 x cotg (0° 35,1') ÷ 1852 = 5,02 millas náuticas.
O también, mediante la segunda fórmula:
D = 1,856 x 95 ÷ 35,1 = 5,02 millas náuticas.
Trazando en la carta náutica la recta correspondiente a la demora verdadera de 300° desde el faro de Espartel, y un arco de circunferencia con centro en dicho faro y radio igual a la distancia calculada de 5,02 millas, la intersección de las dos líneas nos dará la situación:
Latitud = 35° 49,8' N.
Longitud = 006° 00,4' W.
En la sección "Cálculos online" de este blog encontrarás el artículo "Distancia a un punto mediante ángulo vertical" en el que podrás realizar cálculos.
.png)
.png)
0 comentarios:
Publica tu comentario: